Locomotion of self-propelled particles such as motile bacteria or phoretic swimmers often takes place in the presence of applied flows and confining boundaries. Interactions of these active swimmers with the flow environment and the boundaries are important for the understanding of many biological processes, including infection by motile bacteria, the formation of biofilms, and the design of micro and nanomotors for biomedical applications.
The transport behavior of active matter results from the interplay of a multitude of factors including swimming, confinement, and hydrodynamics. Because the transport of biological active matter often occurs in complex domains, our current work focuses on geometries including turtuous domains, fluctuating channels, and random porous media.
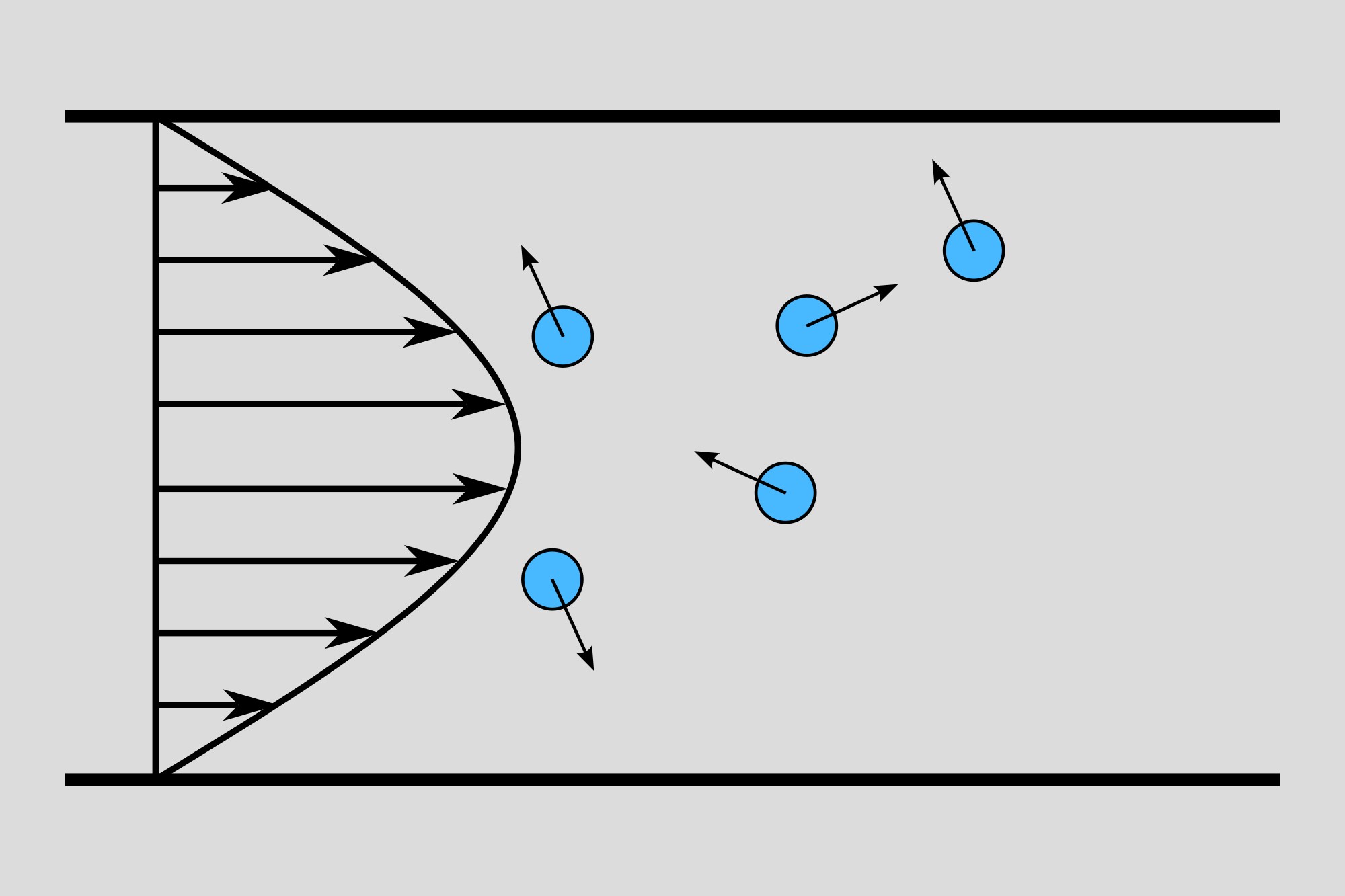
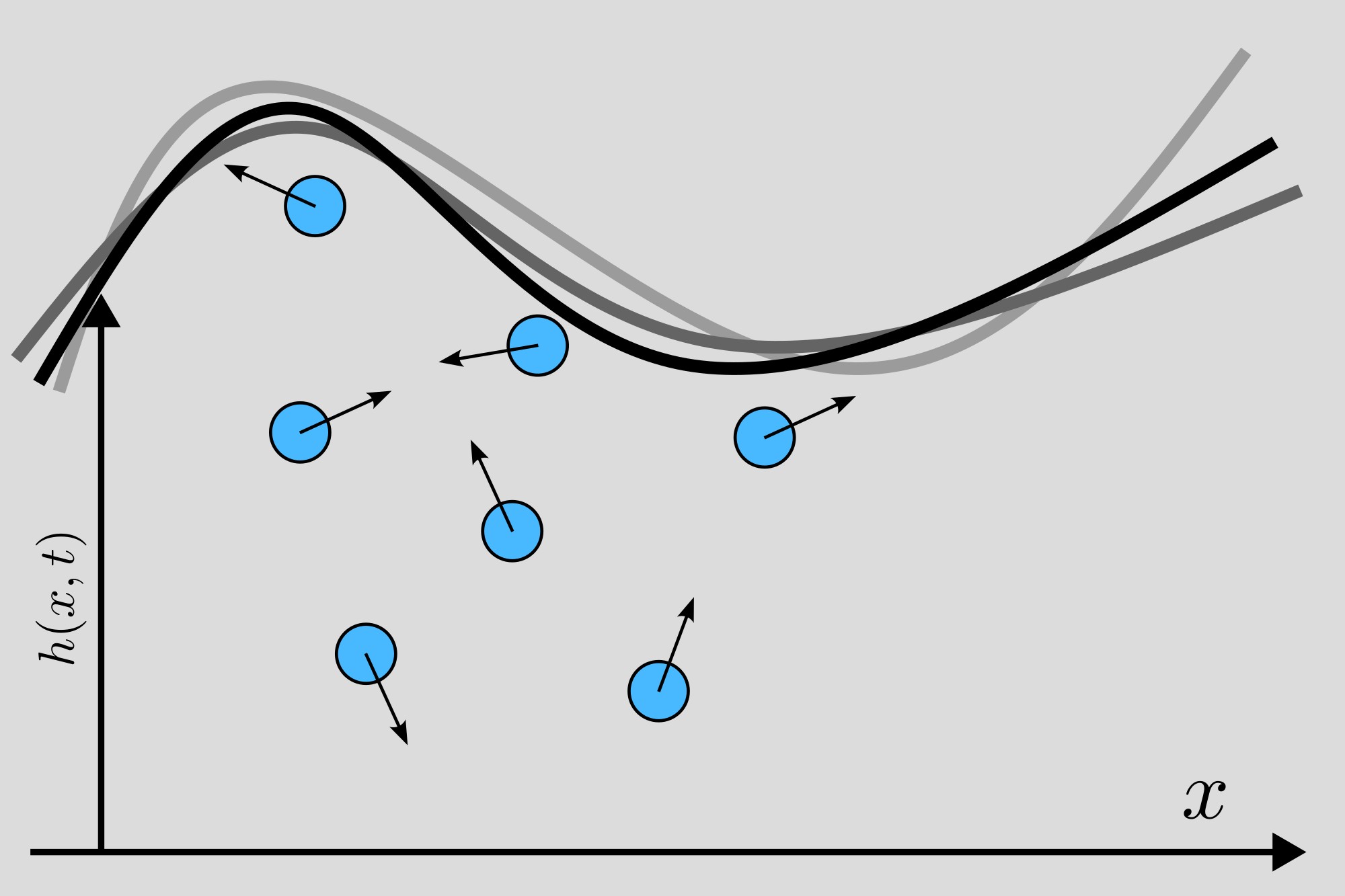
Transport of active particles in Poiseuille flow (left), in a periodic channel (center), and in a time-fluctuating channel (right).
References
2024
-
AI-aided geometric design of anti-infection catheters
Tingtao Zhou, Xuan Wan, Daniel Zhengyu Huang, and 6 more authors
Science Advances, Jan 2024
Bacteria can swim upstream in a narrow tube and pose a clinical threat of urinary tract infection to patients implanted with catheters. Coatings and structured surfaces have been proposed to repel bacteria, but no such approach thoroughly addresses the contamination problem in catheters. Here, on the basis of the physical mechanism of upstream swimming, we propose a novel geometric design, optimized by an artificial intelligence model. Using Escherichia coli, we demonstrate the anti-infection mechanism in microfluidic experiments and evaluate the effectiveness of the design in three-dimensionally printed prototype catheters under clinical flow rates. Our catheter design shows that one to two orders of magnitude improved suppression of bacterial contamination at the upstream end, potentially prolonging the in-dwelling time for catheter use and reducing the overall risk of catheter-associated urinary tract infection. A geometric design provides a simple solution for catheter-associated urinary tract infections.
2022
-
Activity-induced propulsion of a vesicle
Zhiwei Peng, Tingtao Zhou, and John F. Brady
Journal of Fluid Mechanics, May 2022
Modern biomedical applications such as targeted drug delivery require a delivery system capable of enhanced transport beyond that of passive Brownian diffusion. In this work an osmotic mechanism for the propulsion of a vesicle immersed in a viscous fluid is proposed. By maintaining a steady-state solute gradient inside the vesicle, a seepage flow of the solvent (e.g., water) across the semipermeable membrane is generated which in turn propels the vesicle. We develop a theoretical model for this vesicle-solute system in which the seepage flow is described by a Darcy flow. Using the reciprocal theorem for Stokes flow it is shown that the seepage velocity at the exterior surface of the vesicle generates a thrust force which is balanced by the hydrodynamic drag such that there is no net force on the vesicle. We characterize the motility of the vesicle in relation to the concentration distribution of the solute confined inside the vesicle. Any osmotic solute is able to propel the vesicle so long as a concentration gradient is present. In the present work, we propose active Brownian particles (ABPs) as a solute. To maintain a symmetry-breaking concentration gradient, we consider ABPs with spatially varying swim speed and ABPs with constant properties but under the influence of an orienting field. In particular, it is shown that at high activity the vesicle velocity is \bU∼[K_\perp /(\eta_e\ell_m) ]∫\Pi_0^\mathrmswim \bn dΩ, where \Pi_0^\mathrmswim is the swim pressure just outside the thin accumulation boundary layer on the vesicle interior surface, \bn is the unit normal vector of the vesicle boundary, K_\perp is the membrane permeability, \eta_e is the viscosity of the solvent, and \ell_m is the membrane thickness.
2020
-
Upstream swimming and Taylor dispersion of active Brownian particles
Zhiwei Peng, and John F. Brady
Physical Review Fluids, Jul 2020
Locomotion of self-propelled particles such as motile bacteria or phoretic swimmers often takes place in the presence of applied flows and confining boundaries. Interactions of these active swimmers with the flow environment are important for the understanding of many biological processes, including infection by motile bacteria and the formation of biofilms. Recent experimental and theoretical works have shown that active particles in a Poiseuille flow exhibit interesting dynamics including accumulation at the wall and upstream swimming. Compared to the well-studied Taylor dispersion of passive Brownian particles, a theoretical understanding of the transport of active Brownian particles (ABPs) in a pressure-driven flow is relatively less developed. In this paper, employing a small wave-number expansion of the Smoluchowski equation describing the particle distribution, we explicitly derive an effective advection-diffusion equation for the cross-sectional average of the particle number density in Fourier space. We characterize the average drift (specifically upstream swimming) and effective longitudinal dispersion coefficient of active particles in relation to the flow speed, the intrinsic swimming speed of the active particles, their Brownian diffusion, and the degree of confinement. In contrast to passive Brownian particles, both the average drift and the longitudinal dispersivity of ABPs exhibit a nonmonotonic variation as a function of the flow speed. In particular, the dispersion of ABPs includes the classical shear-enhanced (Taylor) dispersion and an active contribution called the swim diffusivity. In the absence of translational diffusion, the classical Taylor dispersion is absent and we observe a giant longitudinal dispersion in the strong flow limit. Our continuum theory is corroborated by a direct Brownian dynamics simulation of the Langevin equations governing the motion of each ABP.